Analitik Geometri Nedir,Özellikleri | Bilim |

Analitik Geometri Hakkında Bilgi,Analitik Geometri Nedir,Geometrik çalışmaya cebrik analizi tatbik eden ve cebrik problemlerin çözümünde geometrik kavramları kullanan bir matematik dalı.

Temel olarak problemleri düzlem geometrisi içinde araştırmaya yönelik tasarlanmasına karşın (iki boyutlu düzlemde geometri), analitik geometri, daha yüksek boyuttaki uzayların incelenmesinde de kullanılabilir.

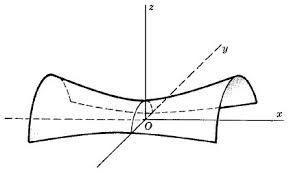
Düzlem analitik geometrisi, konik kesitlerin sistemli biçimde incelenmesini içerir.

Üç boyutun analitik geometrisi, “katı cisimler analitik geometrisi” diye adlandırılır ve dörtyüzlü alanların incelenmesini içerir.

Analitik geometride, noktaların konumları uygun sayı grupları (koordinatlar) aracılığıyla belirtilir; böylece, noktalar arasındaki geometrik ilişki, koordinatları arasındaki cebir ilişkisiyle eşdeğerli olur.

Cebir ile geometri arasındaki bu uygunluk nedeniyle, çoğunlukla geometrik ilişkileri kapsayan önermeler, cebir ilişkileri kullanılarak kanıtlanabilir.

Bu tür cebir tekniklerinin, kuramsal geometri yöntemlerini uygulamada ortadan kaldıracak derecede etkili oldukları kanıtlanmıştır.

Analitik geometrinin temelleri XVII.yy’da Fransız filozofu ve matematikçisi René Descartes tarafından atılmıştır.

Descartes, analitik geometrinin temel ilkelerini felsefe tarihi açısından önemli bir yapıt olan ve kiliseyle herhangi bir tartışmadan kaçınmak amacıyla adını koymadan yayınladığı Metot Üzerine Konuşmalar (Discoursurs de la méthode, 1637) adlı yapıtında açıklamıştır.

Pierre de Fermât da analitik geometri yöntemleri üstünde çalışmış, ama bu konuyla ilgili kitabı, 1679’a kadar yayınlanmamıştır.

Analitik geometrinin günümüzdeki biçimiyse, daha sonra Leonhard Euler tarafından geliştirilmiştir.

Analitik geometri yöntemlerinin doğuşu ve bunun sonucu olarak hesap yöntemlerindeki ilerleme, matematikte, klasik matematikten yeni bir çağa geçişi belirtir.

Analitik geometrinin bulunması, aksiyomların kullanımına dayanan klasik Yunan geometrisinin geliştirilmesinde önemli bir adım olmuştur.

Düzlem Analitik Geometri

Düzlemdeki bir noktanın konumunu belirlemek için, aynı düzlemde kesişen birbirine dik iki doğru (koordinat eksenleri) gereklidir.

Bu eksenlerin kesişme noktası, “orijin” ya da “başlangıç noktası” diye adlandırılır ve O’yla gösterilir.

Genellikle x ekseni başlangıç noktasına yatay, y ekseniyse düşey bir doğrudur.

Pozitif x ekseni başlangıç noktasının sağ tarafı, pozitif y ekseniyse başlangıç noktasının yukarı tarafıdır.

Eksenler, yukarı sağda birinci bölge, saat yönünün tersine aşağı sağda dördüncü bölge olarak, düzlemi dört bölgeye ayırır.

Düzlemde herhangi bir P noktasının x koordinatı (apsis),P’nin y ekseninden dik olan uzaklığıdır; P, y ekseninin sağındaysa “pozitif” (birinci ya da dördüncü bölgede), y ekseninde ise O, y ekseninin solundaysa “negatif” diye adlandırılır.

Benzer biçimde,P’nin y koordinatı (ordinat) P’ninx ekseninden dik olan uzaklığıdır ve “pozitif”, “sıfır” ya da “negatif” olabilir.

P’nin apsisi x, ordinatı y’yse,(x,y)sayı çifti P noktasının değişmez koordinat eksenlerine göre “kartezyen koordinatla-rı”dır (bu ad Descartes’ın anısına verilmiştir).

Örnek olarak (3,-5), dördüncü bölgede üç birim y ekseninin sağında ve beş birim x ekseni altında yer alan P noktasının kartezyen koordinatlarını belirtir.

Her (x,y) gerçek sayı çifti, düzlemde belirli ve karşılıklı tek bir nokta belirtir.

Başlangıç noktası (0,0) dır. (x, y) koordinatlı Pnoktası P(x,y) simgesiyle gösterilir.

Açıklanan bu koordinat sistemine, “dik kartezyen koordinat sistemi” adı verilir.

Eğik koordinat sistemleri bu bölümde incelenmeyecektir.

Kutupsal koordinat sistemi, “başlangıç” ya da “kutup” denilen değişmez bir O noktası ve bu noktadan geçen, “kutup ekseni” denilen değişmez bir eksenden oluşur.

Düzlemde bir P noktası iki niceliği belirtmekle yerleştirilebilir.

(1) Kutup eksenini saat yönünün tersine döndürerek P’den geçmesini sağlayan Ø açısı;

(2) P noktasının başlangıçtan pozitif uzaklığı olan r. Açı değişmez eksen çevresinde dönmeyi sağlayarak bir doğru belirler ve r uzaklığı, başlangıçtan P’ ye ulaşmak için ne kadar birim uzunluk gerektiğini gösterir.

Kutupsal koordinatlarda P noktası, P (r, 0) olarak gösterilir.

Bir kartezyen koordinat sisteminden öbürüne dönüşüm yapmak, ayrıca bir kartezyen sisteminden, kutupsal sisteme karşılıklı dönüşüm yapmak olasılığı her zaman vardır.

Düzlemde P(x,y) noktasının hareket ettirilmesi sonucu oluşan şekil, bir eğridir; x ve y gibi iki değişkenli bir denklem, yalnızca eğri üstündeki noktalar tarafından sağlanıyorsa ve öbür noktalar denklemi sağlamıyorsa, buna “eğrinin denklemi” denir.

Koordinat sistemi sabit olduğundan, bir eğrinin tek bir denklemi vardır ve her denklem tek bir eğriyi belirtir (analitik geometride sağlanan cebir ve geometri arasındaki bağlantı); ax+by+c=0 biçiminde herhangi bir birinci dereceden denklem (a, b ve c), bir doğru denklemidir (ya da doğrusal denklem).

Merkezi başlangıç noktasında ve yarıçapı r olan bir çemberin denklemi x/2+y/2=r/2’dir.

Bir konik kesit x ve y değişkenli ikinci dereceden bir denklemle gösterilebilir, genel denklem; ax/2+bxy+cy/2+dx+ey+f=0’dır(a, b, c, d, e ve f’nin değişmez olması durumunda).

Temel konikler, elips, hiperbol, parabol ve çemberdir.ax+by+c=O ve a’x+b’y+c=O gibi iki doğru yalnızca ve yalnızca ab’— a’b=O olması durumunda paraleldirler ve yalnızca ve yalnızca aa’+bb’ — Oolması durumunda birbirlerine diktirler.

Bir doğru ve birkonikdenklemlerinden x ya da y’nin çekilmesi, dördüncü dereceden bir denklem verir ve yalnızca ve yalnızca, doğru koniğe teğetse, iki kök birbirine eşit olur.

Katı Cisimlerde Anatilik Geometri

Yukarıda özetlenen kavramlar kolaylıkla üç boyutlu uzay için genelleştirilebilir.

Herhangi bir O noktasından (başlangıç noktası) birbirlerine dik üç koordinat ekseni çizilir (x ekseni, y ekseni ve z ekseni); eksenler uzayı sekiz parçaya bölerler; xekseni ve y ekseniyle belirtilen düzlem, xy düzlemidir; xz ve yz düzlemleri de aynı biçimde tanımlanır.

Bu üç düzleme “koordinat düzlemleri” denir.

Bir P noktasının x koordinatı, P’den yz düzlemine dik olan uzaklıktır.

Öbür iki koordinat da benzer biçimde belirtilir; “x,y,z”üçlüsü, x, y ve z koordinatlarıyla P noktasını belirtir; P, birinci bölgedeyse, P’ ninbütün koordinatları ya pozitif ya da sıfırdır.

Böyle bir kartezyen sistemi, “dörtgen kartezyen sistem” diye adlandırılır.

Her nokta tek bir gerçek sayı üçlüsüne karşılık gelir ve her gerçek sayı üçlüsü tek bir noktayı belirtir.

İki çeşit düzlem kutupsal koordinatı vardır: Küresel koordinatlar, silindirsi koordinatlar.